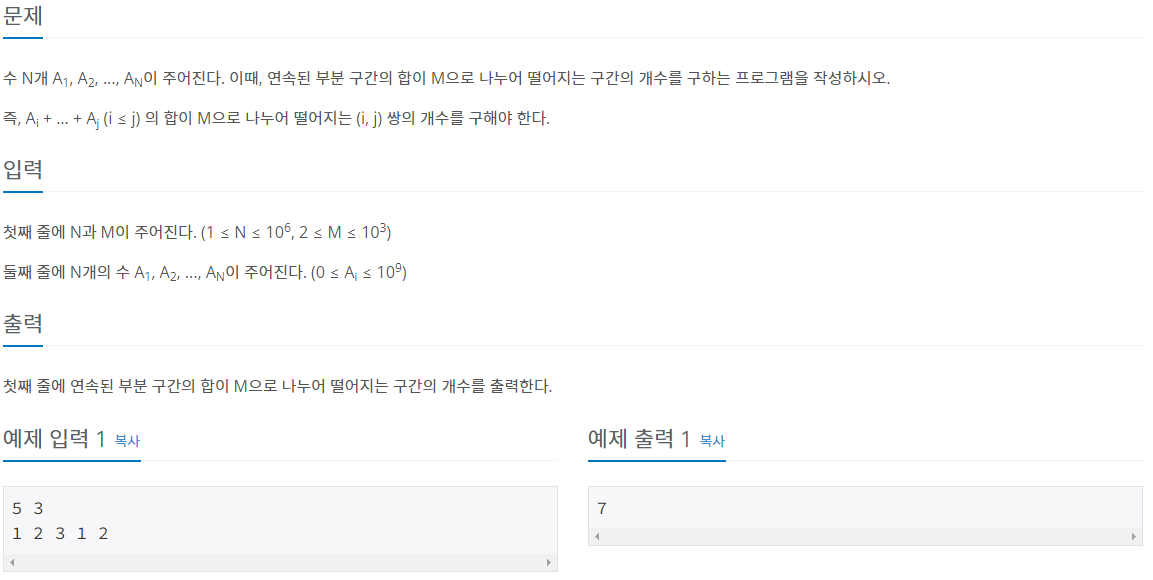
문제
주의
마지막 경우를 세는 변수도 long으로 선언해야 합니다.
10^6개의 경우 중 2개의 경우를 선택하기 때문에 int로 선언하면 오버플로가 발생합니다.
.jpg?type=w800 "막힌 변기, 물빠짐 솔루션을 제공하는 기업 성동구.")
솔루션 프로세스
이 문제는 약 두 달 전에 PS 문제를 막 풀었을 때 누적 합계 알고리즘을 배우면서 한 번 만난 문제입니다.
그 당시에는 모듈식 운영을 활용하는 솔루션을 보고도 이해가 되지 않아 몇 번 시도해보고 합격했습니다.
① 사용할 알고리즘 확인
최대 개수(N)는 10^6이고 지정 시간은 1초(약 10^8 연산)이므로,
이중 for 문 중에 합계를 계산하는 데 시간이 많이 걸립니다.
합계 배열 사용 누적 합계 알고리즘사용
② 번호 범위 확인
숫자의 개수(N)가 최대 10^6이고 숫자의 범위가 최대 10^9이기 때문에
합계의 최대값이 10^15이므로 int를 넘어섭니다.
따라서 합계 배열은 long을 사용합니다.
(향후 오버플로를 방지하려면 int 대신 long을 사용하십시오.)
③ 모듈화 운영 배분법을 이용한다.
(A-B) % M = ((A%M) - (B%M)) % M우리가 찾고 있는 것 (Ai + … + Aj) %M다음에 대한 (i,j) 쌍의 수를 찾으십시오.
이 식을 합계의 배열로 표현하십시오. (S(j) – S(i-1)) %M0과 같은 경우의 수를 찾으려면
모듈러 산술의 분배 법칙을 사용하여 이 방정식을 다시 풀면 다음이 제공됩니다.
((S(j) % M) – (S(i-1) % M)) % M 0과 같은 경우를 찾기 위해
다시 말해서, (S(j) % M) == (S(i-1) % M) 우리의 목표는 ((S(j) % M)과 (S(i-1) % M)의 범위가 0보다 크거나 같고 M보다 작으므로 다음 %M이 생략되는 경우를 찾는 것입니다.
)
④ 나머지 어레이 구축
(S(i) % M)의 값은 0보다 크거나 같고 M보다 작은 값을 갖는다.
나머지가 0이면 인덱스 0을 계산하고 나머지가 1이면 인덱스 1을 계산하는 나머지 배열을 만듭니다.
예시 1로 표현하면 다음과 같다.
⑤ 가능한 쌍의 수를 계산
(1) 나머지가 0인 경우 = 1부터 i까지 입력한 숫자의 합을 의미합니다.
M으로 나뉩니다.
따라서 나머지가 0인 경우의 수를 더하십시오.
(2) 나머지 값이 같은 경우에서 2개를 선택하는 경우
다만, 이 경우 2개 이상의 경우를 도출할 수 있어야 한다.
답변
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String() args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
long() s = new long(N+1);
long() mod = new long(M);
st = new StringTokenizer(br.readLine());
for(int i = 1; i <= N; i++){
int num = Integer.parseInt(st.nextToken());
s(i) = s(i-1) + num;
mod((int)(s(i)%M))++;
}
long count = 0;
count += mod(0);
for(int i = 0; i < M; i++){
if(mod(i) >= 2){
count += (mod(i) * (mod(i)-1)) / 2;
}
}
bw.write(count + "\n");
bw.flush();
bw.close();
}
}
알고리즘 분류
– 수학
– 누적 합계